Estimación De Doble Porosidad Usando Las Curvas De La Derivada
La estimación de los parámetros ω y λ de doble porosidad, se hace en un grafico semi-Log. Ese método semi-Log son frecuentemente impractico, debido a que el efecto de almacenamiento del pozo, esconde la línea recta semi Log en el tiempo temprano. La grafica de la derivada provee un método mucho mas practico para la evaluación de ω y λ. La posición de los mínimos en la derivada (la profundidad que caracteriza el comportamiento de la doble porosidad) define completamente los valores de ambos valores de ω y λ como fue descrito por Bourdet, Ayoub, Whittle, Pirard y Kniazeff (1983). Los mínimos en la derivada pueden ser mostrados que descansan en un valor de la derivada de presión adimensional (Ecuación 6.68) 5:
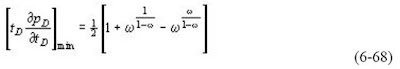
y a un valor del tiempo adimensional de :

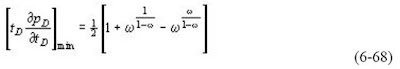
y a un valor del tiempo adimensional de :

Los valores de ω pueden ser evaluados resolviendo la ecuación 6.68 , usando la técnica de Newton- Raspón iterativa mente, después λ el cual puede ser obtenido directamente por la ecuación 6.69 . La determinación iterativa de ω puede ser mucho mas robusta proveyendo al inicio, con un buen primer valor estimado de este. Tal primer estimado puede ser encontrado con la ecuación 6.70:

Figura 6.29 Comparación De Las Ecuaciones 6.69 Y 6.70
La Figura 6.29 muestra una comparación entre las ecuaciones 6.69 y 6.70, y puede ser usada directamente para estimar ω si es requerido.
Como ejemplo de este procedimiento, la Figura 6.30 muestra un grafico de la derivada de una prueba de un pozo en un yacimiento con doble porosidad. La localización de los mínimos es al calor de presión de 1,02 Lpc y a un valor del tiempo de 7 hrs. Usando valores conocidos de q, B, m y h, junto con valores previamente estimados de de K, la derivada de las presiones adimensional a los mínimos pueden ser calculadas, después que los primeros estimados de ω es encontrado por la ecuación (6.70) y un estimado final de ω es encontrado por Newton-Raphson solución de la ecuación (6.68). Después de estimado ω, el valor del tiempo adimensional puede ser calculado usando valores conocidos de f, m, Ct,, y rw junto con valores estimados de K, después λ puede ser estimada usando la ecuación (6.69) ( también requiere de la inclusión de los valores recientes de ω )
Fuente:
Fundamentos de Ingeniería de Yacimientos - Escobar, Fredy H.

